أساليب جمع البيانات في علم الإحصاء

1997 موسوعة الكويت العلمية للأطفال الجزء الثاني

مؤسسة الكويت للتقدم العلمي

علم الإحصاء أساليب جمع البيانات الرياضيات والهندسة الهندسة

إذا طَلبْتَ من كلِّ زميل من زملاء صفِّك في المدرسة أن يذكرَ لك اسمَ الفاكهةِ التي يحبُّها أكثرَ من غيرها من الفواكه فإنك قد تحصل على الإجابات التالية.

وإذا أردتَ أن تستخلصَ من هذه البيانات بعضَ النتائج مثل: اسم الفاكهة التي يحبُّها أكبرُ عدد من زملائك، أو اسم الفاكهة التي يحبُّها أصغرُ عدد من زملائك.

فإنك ترى أن الحاجةَ تدعو إلى تنظيم هذه البيانات في صورة مبسطة واضحة تجعل دراستَها سهلةً ومُيَسَّرةً. وهنا عليك أن تلجأ إلى الإحصاء.

 

والبيانات التي حَصَلْتَ عليها من زملائك يمكن وضعُها في جدول يُبرزُ هذه البياناتِ بأكبر وضوح ممكن.

وفي أضيق حَيِّز، وبصورة مرتبة ومختصـرة تهيّئ لك السبيلَ إلى فهمِها والوصولِ إلى النتائج منها، وذلك على النحو التالي:

 

ومن السهل عليك الآن أن تستخلصَ بعضَ النتائج من هذا الجدول مثل.

– الفاكهةُ التي يحبها أكبرُ عدد من زملائكَ، هي الموز.

– الفاكهةُ التي يحبها أصغرُ عدد من زملائك، هي التفاح.

– عددُ الزملاء الذي يحبون البرتقالَ أكبرُ من عدد الزملاء الذين يحبون العنب.

 

وقد يَصْعُبُ على بعض الناس فهم البيانات في صورة جداول، ولذلك يُمِدُّنا الإحصاء بأسلوب آخر يؤدي إلى زيادة وضوح البيانات وسهولةِ فهمها. هذا الأسلوبُ الآخر هو أسلوبُ الرسم والتصوير، أي أسلوبُ العرض البياني.

ومن طرق العرض البياني في الاحصاء ما يلي:

– الرسومُ التصويرية.

– الرسومُ ذات الأعمدة.

– الرسومُ القطاعية.

 

ولاستخدام الرسم البياني التصويري لعرض إجابات زملائك عن اسم الفاكهة المحبَّبة لدى كلٍّ منهم نكتبُ أسماء الفواكه المحببة لهم في الجهة اليمنى من الصفحة.

ثم نقرأ الإجابات المعطاة من قِبَل الزملاء واحدة بعد الأخرى ونستبدل كل إجابة بالشكل ….، الذي يمثل زميلاً واحدا، ونرسمه في الجهة اليسرى أمام اسم الفاكهة الذي أشارت إليه الإجابةُ مع مراعاة تساوي المسافات بين الأشكال عند رسمها، فنحصل على الرسم البياني التصويري التالي:

 

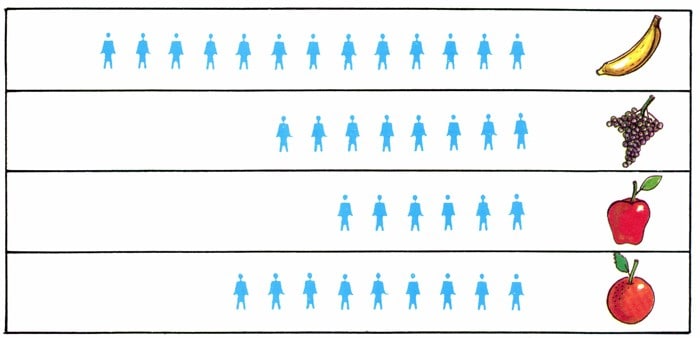
ونلاحظ أن وسيلةَ العرضِ هذه أوضحُ كثيرا في تمثيل البيانات من عرضها في جدول، وإذا أردنا زيادةَ الوضوح والدقة في عرض البيانات فإننا نستخدم أشكالاً هندسية للتمثيل بالرسم.

وأكثرُ هذه الأشكال استخداما المنطقةُ المستطيلة وتسمى هذه الرسومُ في الاحصاء بالرسوم البيانية ذاتِ الأعمدة.

ولعرض إجابات زملائك بواسطة الأعمدةِ نتخذُّ مِحْوَرَيْن أحدُهما أفقيٌّ نحدد عليه أسماء الفواكه المحببة لديهم والآخر رأسي يمثل عدد الزملاء.

ثم نحدد على المحور الأفقي مسافاتٍ متساويةً تمثل أسماءَ الفواكه المحبة لدى الزملاء، ثم نرسم مناطق مستطيلة قواعدُها هذه المسافاتُ وارتفاعاتها تمثل أعداد الزملاء الذين يحبون هذه الفواكه، ونحصلُ على الشكل البياني ذي الأعمدة التالي:

 

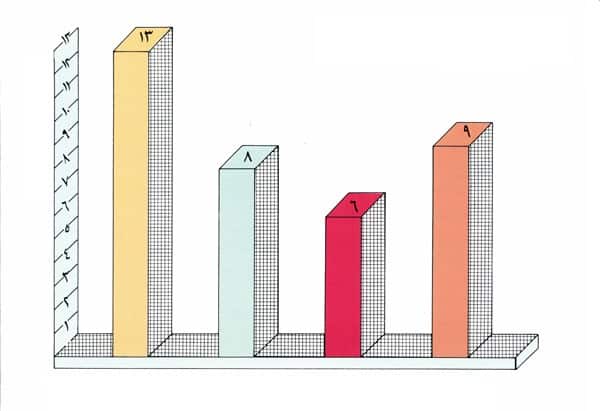
ويتبين لنا أن استخدام الأعمدة يعطي فكرة سريعةً وواضحةً عن البيانات حيث كلُّ عمود يمثل شيئا معينا. ونظرا لأن المناطقَ المستطيلة متساوية في القاعدة فإن المقارمة تكون بين ارتفاعاتها فقط.

ولذلك تُستخدم الأعمدة بصفة أساسية للمقارنة بين عددٍ من الكميات وخاصةً فيما يتعلقُ بأمور من المهم دراسةُ تطورها مع الزمن مثل عدد السكان، أو مقدارِ إنتاج النفط، أو الصادرات والواردات للدولة.

 

وفي الإحصاء يمكننا أيضا أن نستخدمَ الدوائرَ في الرسوم البيانية القطاعية.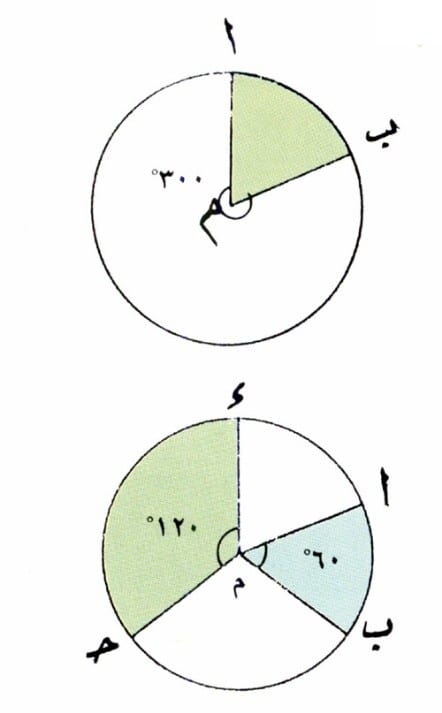

ففي الشكل الأوَّل يمثل الجزء المُلَوَّن أ م ب قطاعا في الدائرة زاويته المركزية 60°(من الزاوية المركزية الكلية التي قياسها العددي 360°).

أما في الشكل الثاني فمساحة القطاع الدائري أ م ب = ½ مساحة القطاع الدائري م ح د الذي فيه الزاوية المركزية قياسها عدديا هو 120°.

 

وهذا يعني أن النسبة بين مساحات القطاعات الدائرية المختلفة في الدائرة الواحدة كالنسبة بين القياسات العددية لزواياها.

وبذلك يهسلُ تقسيمُ الدائرةِ إلى الأجزاء المطلوبة التي تتنـاسبُ مع أي أعداد. فما عليـنا عندئـذ إلا تقسيمُ الزاوية المركزية الكلية للدائرة التي قياسُها عدديا هو 360°إلى زوايا تتناسب قياساتها العددية مع هذه الأعداد، ثم نرسم قطاعاتٍ دائريةً لها هذه الزوايا.

ولاستخدام الرسم البياني القطاعي لتمثيل إجابات زملائك، نرسم دائرةً ثم نقوم بتقسيم الزواية المركزية الكلية التي قياسُها عدديا هو360°على 36، وهو عدد زملاء صفك، فنحصل على زاوية مركزية قياسها عدديا هو°10

 

وحيث أن عددَ الزملاء الذين يفضلون الموز هو 13°فلتكون الزاوية المركزية للقطاع الدائري الذي يمثلُّهم ذات قياس عددي هو 130°.

وبالمثل تصبح الزوايا المركزية للقطاع الذي يمثل من يُفَضِّلون العنبَ هي 80°، والذين يفضلون التفاح 60°والذين يفضلون البرتقال 90°، كما هو مبين في الرسم التالي:

 

وهكذا يتضح لنا أن الإحصاءَ علمٌ يبحث فيما يلي:

– طرقُ تجميع البيانات.

– كيفية تسجيل البيانات في صورة عددية.

– طرقُ تلخيص البيانات وترتيبها وعرضها بطريقة يسهلُ بها تفسيرُها والحصولُ منها على النتائج.

 

ومن الإحصاء نعرف أن البيانات يمكن ترتيبها وعرضها بصورة ميسرة بإحدى صورتين هما:

– العرضُ الجدولي يوضح البيانات في جداول.

– العرضُ البياني وذلك بواسطة رسوم بيانية.

 

ونلاحظ في وقتنا الحالي أن الصحفَ والمجلات والبرامج التلفزيونية وغيرَها من وسائل الإعلام تَزْخَرُ بالعديد من المعلومات والبيانات في صورة جداول ورسوم إحصائية والتي تَهْدُفُ إلى تصوير الظروف والنتائج والتوقُّعاتِ لمجالات النشاط البـشـري المختلفة، مثل التجارة والزراعة والصناعة.

وهذا أمر يشير إلى اتساع استخدام علم الإحصاء في جميع نواحي حياة المجتمع. وذلك يمكن القولُ بأن دراسةَ علم الإحصاء والإلمام بأسسه وأساليبه يُعَدُّ من الأمور المهمة والمفيدة لإنسان العصر الحالي.

[KSAGRelatedArticles] [ASPDRelatedArticles]